Gradients
Contents
Gradients#
Over the next few lectures we will build from calculating gradients (which many of you have seen) to using gradient descent to find local maxima/minima, to exploring and implementing algorithms for gradient descent.
Review of Derivatives#
The importance of the derivative is based on a simple but important observation.
While many functions are globally nonlinear, locally they exhibit linear behavior. This idea is one of the main motivators behind differential calculus.
Consider this smooth function:
The closer we zoom in on it, the more it looks like a line.
The derivative \(f'(x)\) of a function \(f(x): \mathbb{R}\rightarrow\mathbb{R}\) is the slope of the approximating line, computed by finding the slope of lines through closer and closer points to \(x\):
In other words, the derivative of a function at a point is basically its slope at that point.
Partial Derviatives#
Now, our goal is going to be to apply this notion of “slope” to functions of more than one variable – that is, functions of vectors.
If a function \(f\) takes multiple inputs, then it can be written
In other words, for each point \(\mathbf{x} = \begin{bmatrix}x_1\\\vdots\\x_n\end{bmatrix}\) in \(n\)-dimensional space, \(f\) assigns a single number \(f(x_1, \dots, x_n)\).
For example, for \(f(\mathbf{x}): \mathbb{R}^2 \rightarrow \mathbb{R}\), we can think of \(f\) as defining a surface in three dimensions.
Here is an example function:
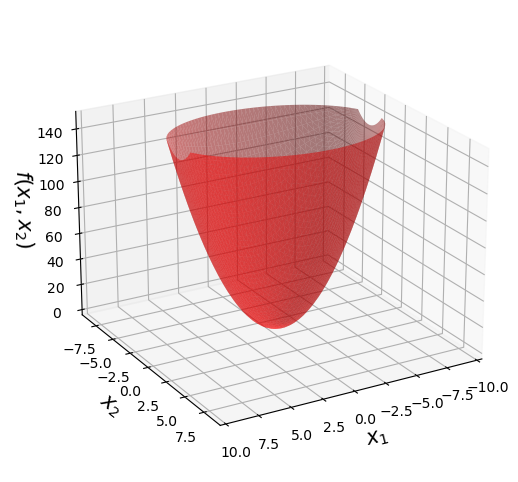
At first it may seem hard to apply the notion of linearity to a surface, since a line is a 1-D concept.
However, if we fix all but one variable, the function becomes a simple line again: \(\mathbb{R}\rightarrow\mathbb{R}\).
So we will isolate each variable and study it separately.
That means, we focus on one variable, and think of all other variables as constants.
This leads to a definition:
Partial Derivative. The partial derivative of \(f\) with respect to \(x\) is given by differentiating \(f\) with respect only to \(x\), holding the other inputs to \(f\) constant.
The partial derivative of \(f\) with respect to \(x\) is written
For example, consider the \(f\) above:
To take the partial derivative of \(f\) with respect to \(x_1\), treat the occurrences of \(x_2\) as if they were “just numbers”.
So
And
Here is a visualization of the partial derivative with respect to \(x_1\).
Consider the case where \(x_2 = 3.\) Then we are looking at the 1D curve defined by the intersection of the plane \(x_2 = 3\) and the function \(f\).
