Maximum Likelihood Estimation

Maximum likelihood estimation is one of the most useful tools for parameter estimation. The technique is intuitive and has nice theoretical properties that make it the most popular method for learning parametric models.

Today’s lecture builds upon our previous lecture, model fitting. We will shortly review it but refer to the previous section for mathematical details.

The Maximum Likelihood Principle

We have seen some examples of estimators for parameters in the first lecture on parameter estimation. But where do estimators come from exactly?

Rather than making guesses about what might be a good estimator, we’d like a principle that we can use to derive good estimators for different models.

The most common principle is the maximum likelihood principle.

The Maximum Likelihood Estimate (MLE) of \(\theta\) is that value of \(\theta\) that maximizes the likelihood function - that is, makes the observed data “most probable” or “most likely”.

Formally, we say that the maximum likelihood estimator for \(\theta\) is:

\[ \hat {\theta}_{\text{ML}} = \arg \max_\theta p(X_s; \theta), \]

which for a dataset of \(m\) items is:

\[ \hat {\theta}_{\text{ML}} = \arg \max_\theta \prod_{i=1}^m p(x_i; \theta). \]

This is the same thing as maximizing the log-likelihood:

\[ \hat \theta_{\text{ML}} = \arg \max_\theta \log p(X_s; \theta) = \arg \max_\theta \sum_{i=1}^m \log p(x_i; \theta). \]

We will drop the ML subsript in the remaining part of the lecture.

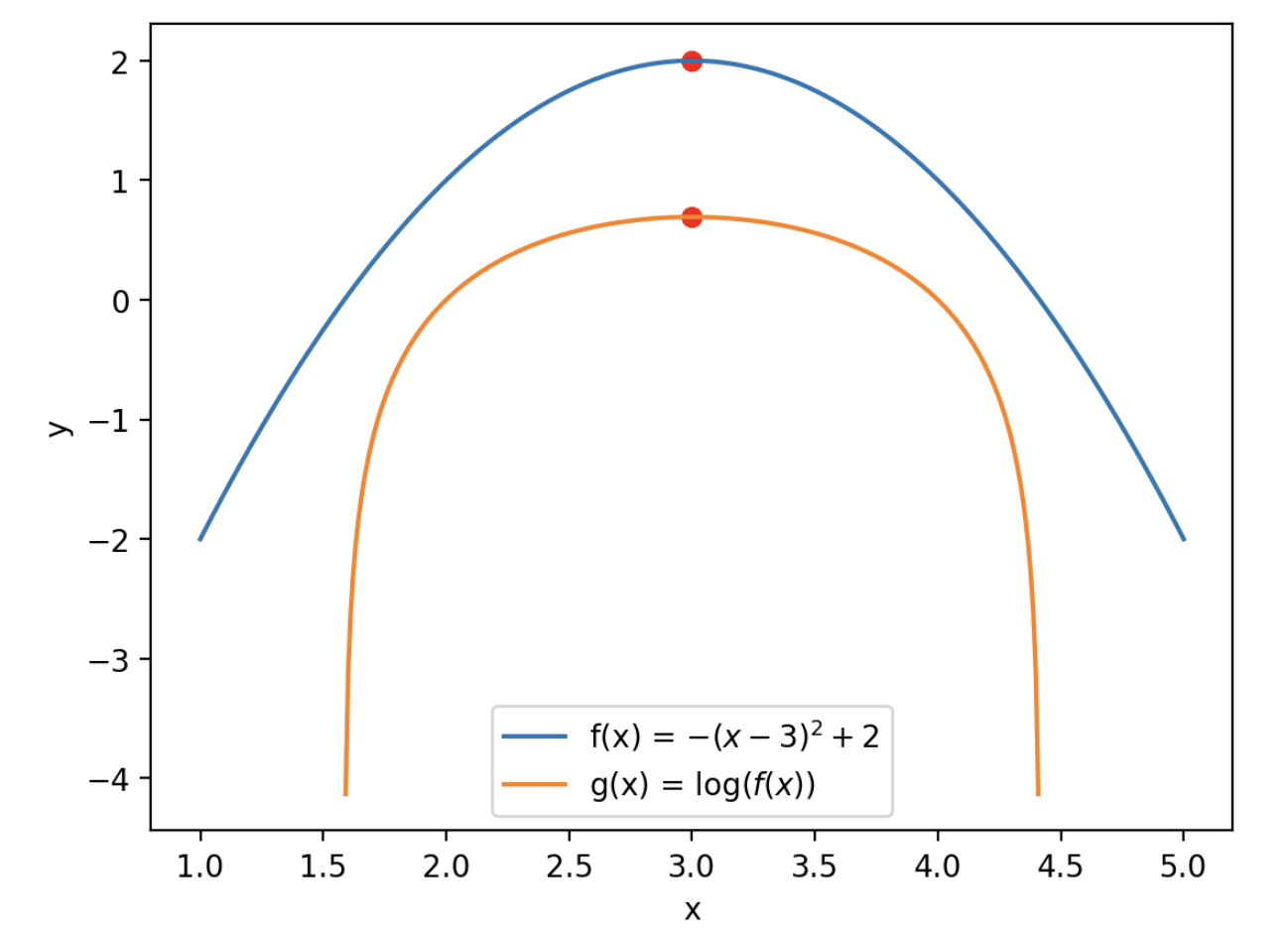
Since \(\log\) is a monotonic function, the likelihood function and the log-likehood function have maxima in the same location.

Illustration of this property for a general (i.e., not likehood function) function \(f(x)\) and its natural logarithm \(g(x) = \log f(x)\):

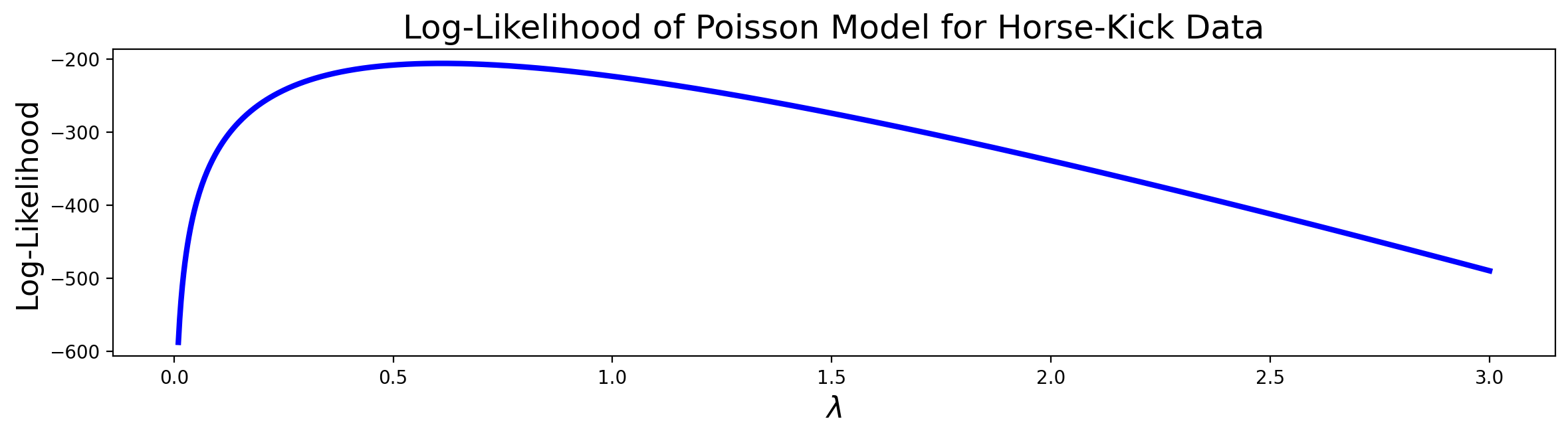
Example. Looking back at the deaths-by-horse-kick data, we can see that there is clearly a maximum in the plot of the log-likelihood function, somewhere between 0.5 and 1.

If we use the value of \(\theta = \lambda\) at the maximum, we are choosing to set \(\lambda\) to maximize the (log-)likelihood of the data under the model.

Computation of MLE

Often, the MLE is found using calculus by locating a critical point:

\[\frac{\partial}{\partial \theta} \log p(X_s; \theta) = 0 \text{ and } \frac{\partial^2 }{\partial \theta^2}\log p(X_s; \theta)<0.\]

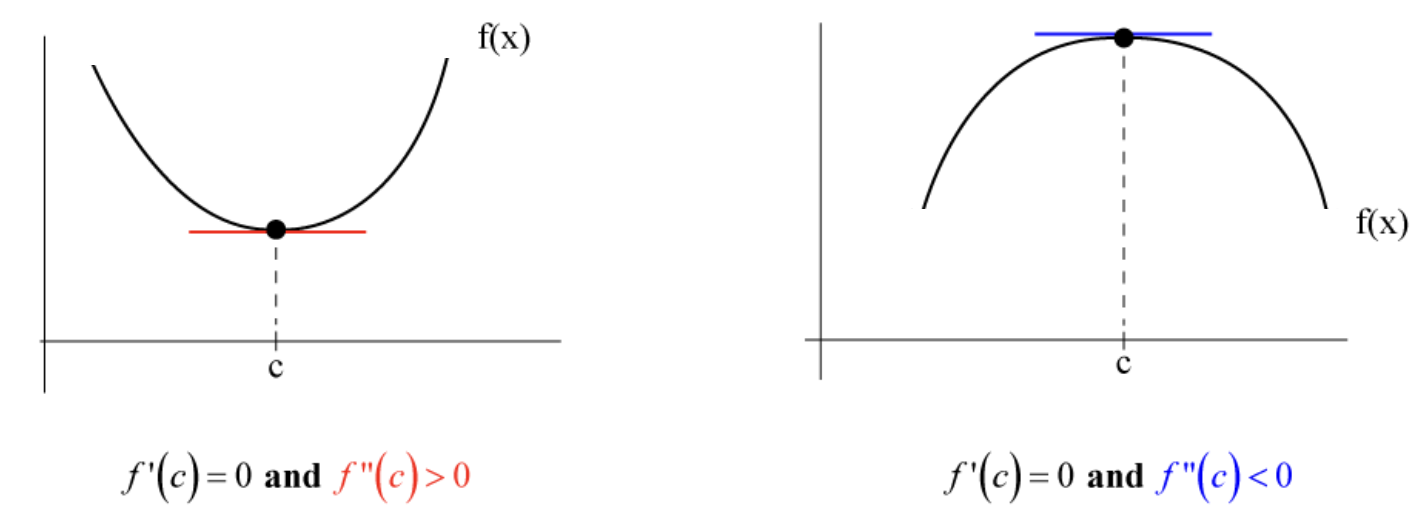
The computation of the second derivatives becomes reduntant when the graph of the log-likelihood function is available and confirms that the critical point is indeed a maximum.

The table below shows some useful properties of the derivatives.

Natural logarithm	\(\frac{d}{dx}\log x = \frac{1}{x}\)
Product rule	\(\frac{d}{dx}(uv) = u\frac{dv}{dx} + v\frac{du}{dx}\)
Quotient rule	\(\frac{d}{dx}\left(\frac{u}{v}\right) = \frac{v\:du/dx\:-\:u\:dv/dx}{v^2}\)
Chain rule	\(\frac{d}{dx}z(y(x)) = \frac{dz}{dy}\frac{dy}{dx}\)

Summary of the computational steps

The steps to find Maximum Likelihood Estimate \(\hat{\theta}\) for distribution parameter \(\theta\):

1. Compute the likehood function \(p\left(X_s;\theta \right).\)
   

2. Compute the corresponding log-likelihood function \(\log p\left(X_s;\theta \right).\)
   

3. Take the derivative of the log-likelihood function with respect to \(\theta\).
   

4. Set the derivative to zero to find the MLE.
   

5. (Optional) Confirm that the obtained extremum is indeed a maximum by taking the second derivative or from the plot of the log-likelihood function.

Example.

Previously we looked at the following problem:

Suppose that \(x\) is a discrete random variable with the probability mass function shown below.

\(x\)	\(0\)	\(1\)	\(2\)	\(3\)
\(p(x;\theta)\)	\(\frac{2}{3}\theta\)	\(\frac{1}{3}\theta\)	\(\frac{2}{3}\left(1-\theta\right)\)	\(\frac{1}{3}\left(1-\theta\right)\)

Here \(0\leq \theta \leq 1\) is a parameter. The following 10 independent observations were taken from this distribution:

\[X_s = (3,0,2,1,3,2,1,0,2,1).\]

Before we found the corresponding log-likelihood function. This time we want to go a step further and find the MLE for \(\theta\).

We know that the likelihood function is equal to

\[p(X_s;\theta) = \prod_{i=1}^{10} p\left(x_i; \theta\right)=\left( \frac{2}{3}\theta \right)^2 \left( \frac{1}{3}\theta \right)^3 \left(\frac{2}{3}\left(1-\theta\right)\right)^3 \left(\frac{1}{3}\left(1-\theta\right)\right)^2.\]

This function is not easy to maximize. Let us look at the log-likelihood function.

The log-likelihood function is given by

\[\log p(X_s;\theta) = \sum_{i=1}^{10}\log p\left(x_i;\theta \right) = 5\log \theta + 5\log (1-\theta) + 5\log\frac{2}{9}.\]

The derivative of the log-likelihood function with respect to \(\theta\) is equal to

\[\frac{\partial}{\partial\theta}\log p(X_s;\theta) = \frac{5}{\theta} - \frac{5}{1-\theta}.\]

Setting the derivative to zero leads to

\[5(1-\theta) - 5\theta=0,\]

\[1-2\theta=0.\]

This suggests that the MLE for \(\theta\) is potentially \(\hat{\theta}=\frac{1}{2}.\)

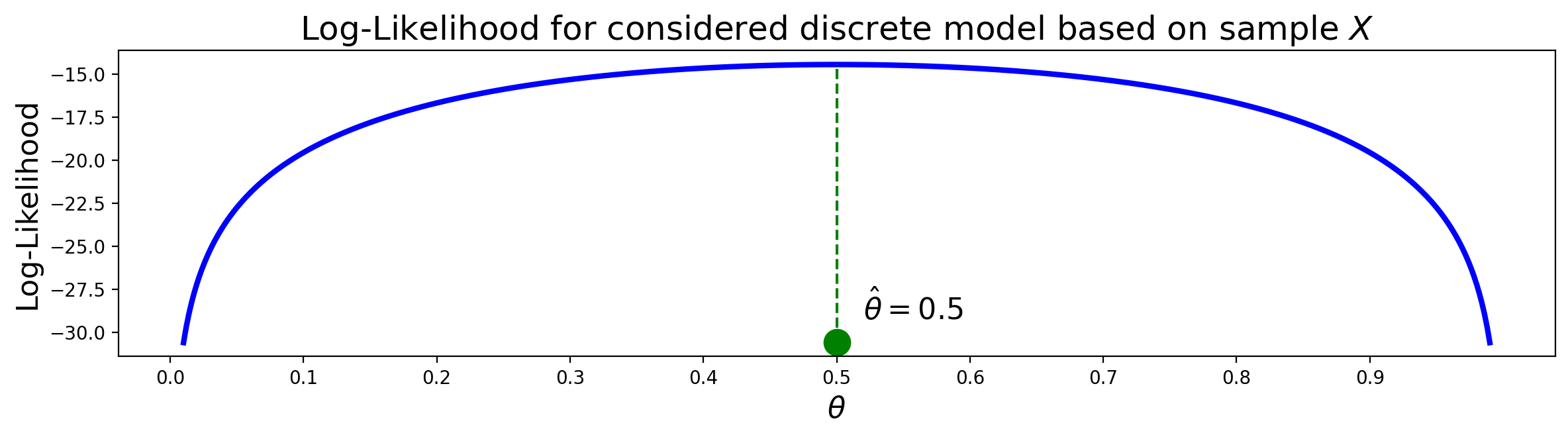
The figure shows that \(\hat{\theta}=\frac{1}{2}\) is a maximum. Therefore, the MLE of \(\theta\) is indeed \(\frac{1}{2}.\)

Example.

Let’s revisit the Bortkeiwicz’s horse-kick data as well. Recall that Bortkeiwicz had collected deaths by horse-kick in the Prussian army over a span of 200 years, and was curious whether they occurred at a constant, fixed rate.

Deaths Per Year	Observed Instances
0	109
1	65
2	22
3	3
4	1
5	0
6	0

Previously we started fitting the data to a Poisson distribution. We found that the likelihood function is given by

\[p(X_s;\lambda) = \prod_{i=1}^{m} \lambda^{x_i} \frac{e^{- \lambda}}{x_i!}.\]

From the likelihood function we obtained the log-likehood function:

\[\log p(X_s; \lambda) = \log \left( \prod_{i=1}^{m} \lambda^{x_i} \frac{e^{- \lambda}}{x_i!} \right) = \sum_{i=0}^m \left( x_i \log \lambda - \lambda - \log x_i!\right).\]

To find the maximum of the log-likelihood of the data as a function of \(\lambda\), we need to compute the derivative w.r.t. \(\lambda\):

\[ \frac{\partial}{\partial\lambda}\log p(X_s; \lambda) = \frac{\partial}{\partial\lambda} \sum_{i=0}^m \left( x_i \log \lambda - \lambda - \log x_i!\right)\]

\[=\sum_{i=0}^m \left(x_i \frac{1}{\lambda} - 1 \right) = \frac{1}{\lambda}\sum_{i=0}^m x_i - m. \]

Setting the derivative to zero, we get the expression for the maximum likelihood estimator

\[\frac{1}{{\lambda}}\sum_{i=0}^m x_i - m = 0,\]

\[{\hat{\lambda}} = \frac{1}{m}\sum_{i=0}^m x_i.\]

This is just the mean of the data, that is, the average number of deaths per year! From the available data we can compute that the mean is 0.61. The plot confirms that 0.61 is indeed a maximum. Therefore, the MLE of \(\lambda\), \(\hat{\lambda}\) = 0.61.

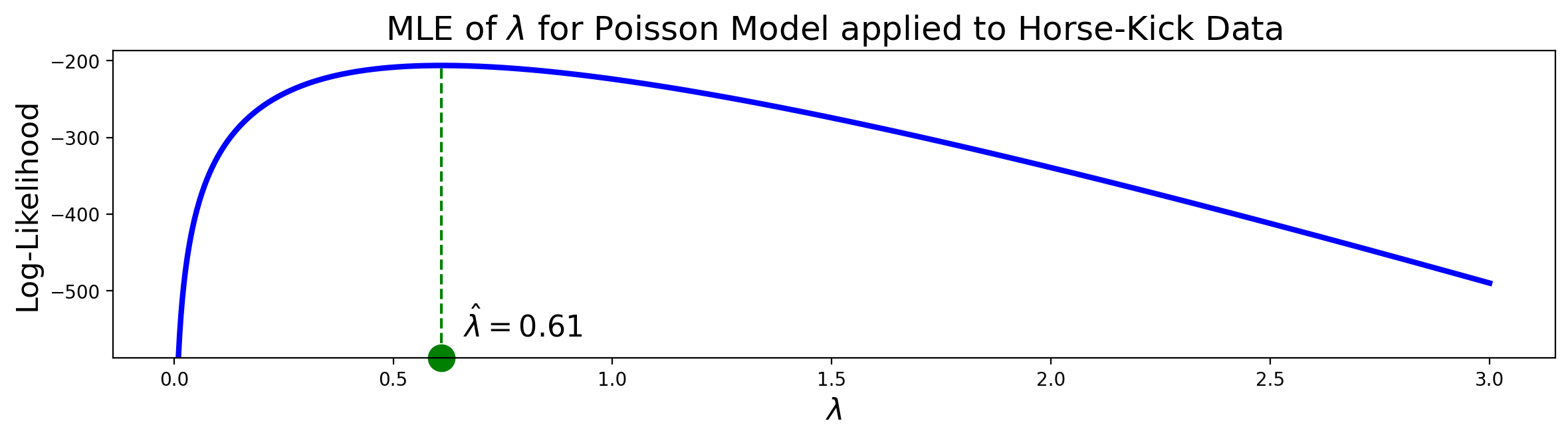
The plot confirms that 0.61 is indeed a maximum. Therefore, the MLE for \(\lambda\), \(\hat{\lambda}\) = 0.61.

Using this estimate for \(\lambda\), we can ask what the expected number of deaths per year would be, if deaths by horse-kick really followed the assumptions of the Poisson distribution (ie, happening at a fixed, constant rate):

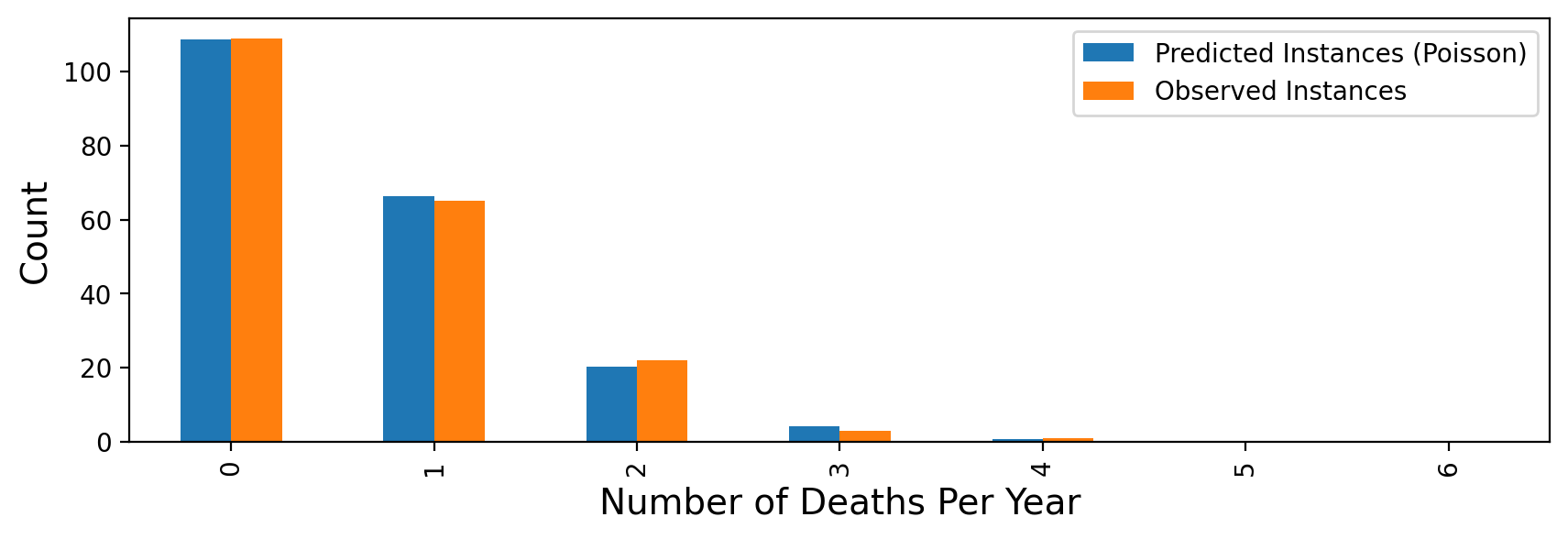
Which shows that the Poisson model is indeed a very good fit to the data!

From this, Bortkeiwicz concluded that there was nothing particularly unusual about the years when there were many deaths by horse-kick. They could be just what is expected if deaths occurred at a constant rate.

Example.

We also had looked at sample data \(X_s =(x_1, \dots, x_m)\) from a normal distribution \(N(\mu,\sigma^2)\) with \(\mu\) and \(\sigma\) unknown. To fit the data to a normal distribution both \(\mu\) and \(\sigma\) have to be estimated.

We found previously that the likelihood function is equal to

\[p\left(X_s; \mu, \sigma\right)= \left(\frac{1}{\sigma \sqrt{2\pi}}\right)^m \exp\left(\sum_{i=1}^m -\frac{1}{2}\left(\frac{x_i - \mu}{\sigma} \right)^2 \right),\]

while the log-likelihood function is given by

\[\log p\left(X_s; \mu, \sigma \right) = -m\log \sigma - \frac{m}{2}\log(2\pi) -\frac{1}{2\sigma^2}\sum_{i=1}^m \left(x_i - \mu \right)^2.\]

Replacing the constant term by \(c\) we can write the log-likehood as

\[\log p\left(X_s; \mu, \sigma \right) = -m\log \sigma -\frac{1}{2\sigma^2}\sum_{i=1}^m \left(x_i - \mu \right)^2+c.\]

The partials with respect to \(\mu\) and \(\sigma\) are

\[\frac{\partial}{\partial \mu} \log p\left(X_s; \mu, \sigma \right) = - \frac{1}{2\sigma^2}\sum_{i=1}^m 2(-1)\left(x_i-\mu\right) = \frac{1}{\sigma^2}\sum_{i=1}^m \left(x_i-\mu\right),\]

\[\frac{\partial}{\partial \sigma} \log p\left(X_s; \mu, \sigma \right) = -\frac{m}{\sigma} + \frac{1}{\sigma^3}\sum_{i=1}^m \left(x_i - \mu \right)^2.\]

We assume that \(\sigma>0\) and set the first partial derivative to zero:

\[\frac{1}{\sigma^2}\sum_{i=1}^m \left(x_i-\mu\right)=0 \Leftrightarrow \sum_{i=1}^m x_i - m\mu = 0 \Leftrightarrow \mu = \frac{1}{m}\sum_{i=1}^m x_i.\]

Thus, \(\hat{\mu}\) is the sample mean.

To find an estimate for the standard deviation we use \(\hat{\mu}\) and set the second partial derivative to zero. Since \(\sigma>0\), we obtain

\[-\frac{m}{\sigma} + \frac{1}{\sigma^3}\sum_{i=1}^m \left(x_i - \hat{\mu} \right)^2=0 \Leftrightarrow \frac{1}{\sigma^2}\sum_{i=1}^m \left(x_i - \hat{\mu} \right)^2=m \]

\[\Leftrightarrow \sigma = \sqrt{\left(\frac{1}{m}\sum_{i=1}^m \left(x_i - \hat{\mu} \right)^2\right)},\]

where \(\hat{\mu}\) is the sample mean.

Thus, the potential MLE for \(\mu\) and \(\sigma\) are

\[\hat{\mu} = \frac{1}{m}\sum_{i=1}^m x_i,\]

\[\hat{\sigma} = \sqrt{\left(\frac{1}{m}\sum_{i=1}^m \left(x_i - \hat{\mu} \right)^2\right)}.\]

The upcoming Python example will illustrate that the above \(\hat{\mu}\) and \(\hat{\sigma}\) are indeed maxima and hence are the MLE for \(\mu\) and \(\sigma\) of \(N(\mu,\sigma^2)\).

Visualizing MLE

We look at a sample of size 100 from a normal distribution. The log-likelihood function can be created in the following way.

# log-likelihood function for a normal distribution
# input: sample, parameters' domains
def normloglik(X,muV,sigmaV):
    m = len(X)
    return -m/2*np.log(2*np.pi) - m*np.log(sigmaV)\
    - (np.sum(np.square(X))- 2*muV*np.sum(X)+m*muV**2)/(2*sigmaV**2)

The MLE for \(\mu\) and \(\sigma\) can be computed using the mean and var functions from NumPy.

# MLE for the mean and the standard deviation
mu_hat  = np.mean(data)
sig_hat = np.sqrt(np.var(data, axis = 0, ddof = 0))
llik    = normloglik(data, mu_hat, sig_hat)

We can visualize the MLE on the surface plot.

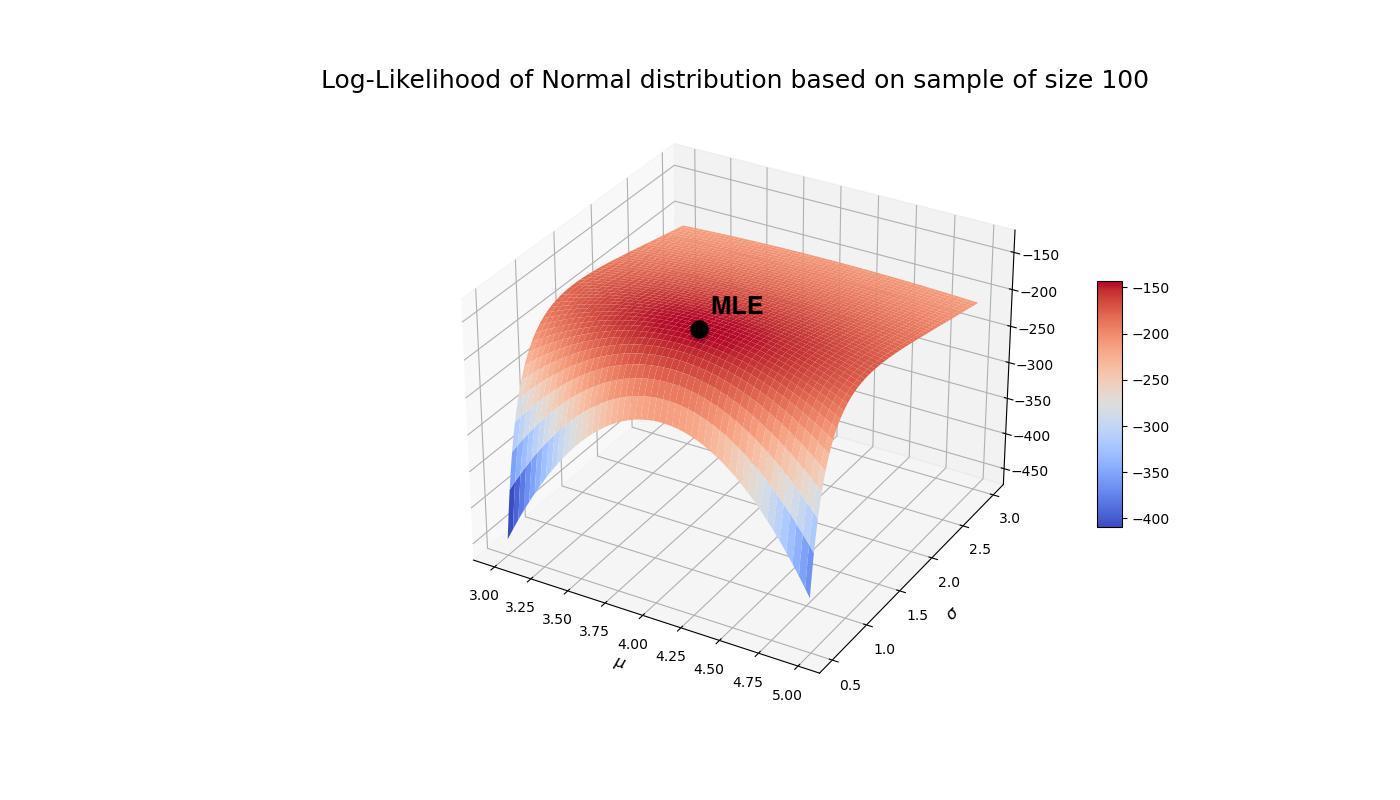
Alternatively, if one of the parameters is known, we visualize the log-likelihood as function of the unknown parameter and indicate the computed MLE.

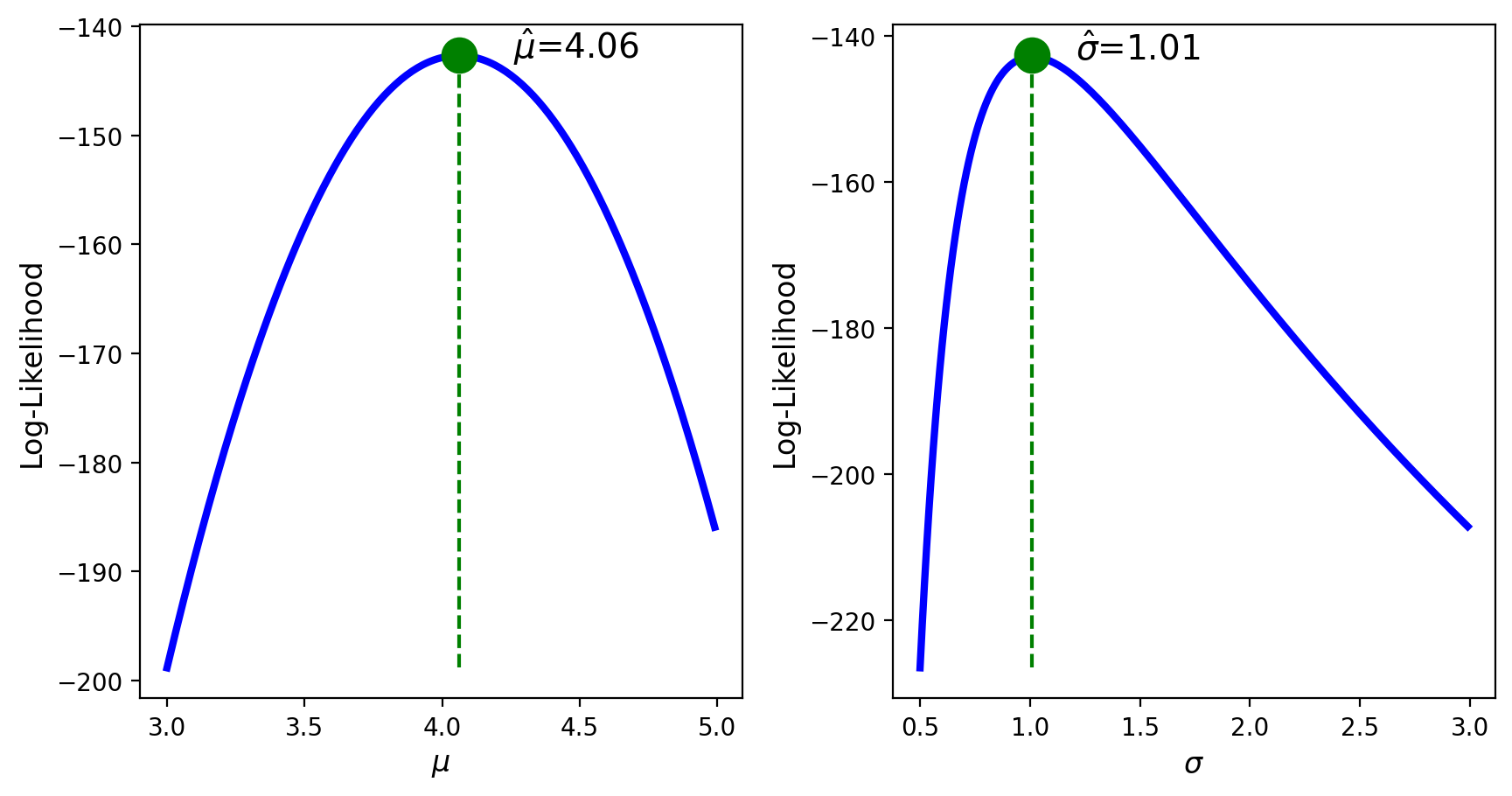
Consistency

The maximum likelihood estimator has a number of properties that make it the preferred way to estimate parameters whenever possible.

In particular, under appropriate conditions, the MLE is consistent, meaning that as the number of data items grows large, the estimate converges to the true value of the parameter. We will introduce the concept of consistency more precisely in one of the future lectures.

For now we are going to focus on the fact that it can be shown that for large sample sizes, no consistent estimator has a lower MSE than the maximum likelihood estimator.