Markov Chains

Markov Chains#

Today we will take a temporary pause from Bayesian statistics to discuss a fundamental tool in probability.

Consider the following model for the weather in Boston:

If today is sunny, tomorrow will be sunny with probability 0.8; otherwise it will be rainy. If today is rainy, tomorrow will be rainy with probabililty 0.6; otherwise it will be sunny.

We can draw this scenario with a diagram like this:

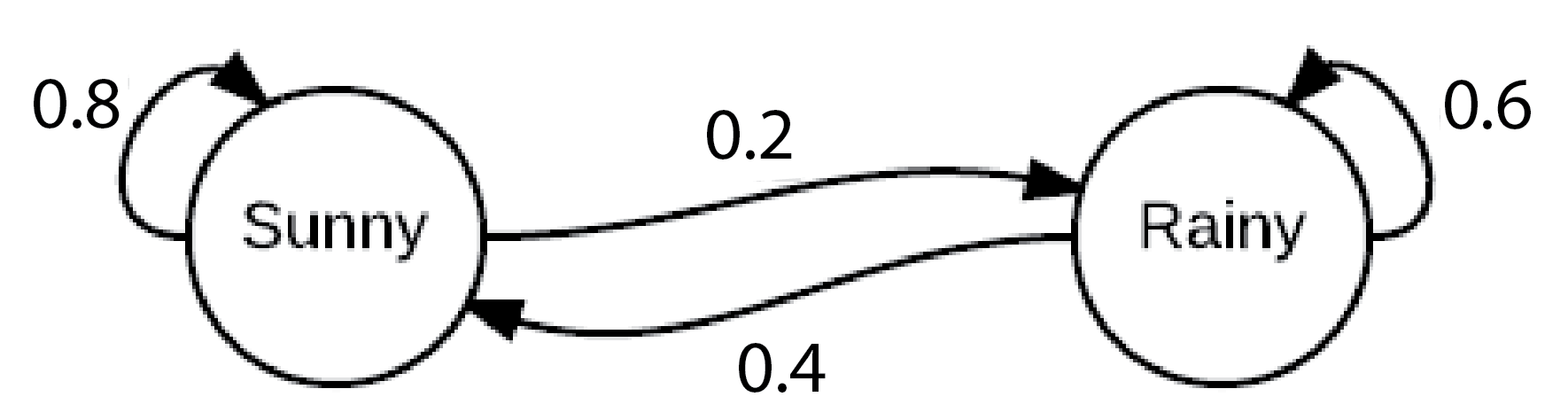
Why is this useful? It helps us reason about what might happen many days in the future.

For example, we can ask “what is the probability that if today is sunny, tomorrow is sunny and the day after this is rainy” by imaging taking a walk along this graph following the arrows, and multiplying the probability each time.

The great thing is we can do this at the same time for all possible starting conditions for an aribtrary number of days into the future! We’ll do this by combining our knowledge of linear algebra and probability.

This tool is called the Markov Chain after its inventor Andrei Markov, a Russian mathematician working in the late 19th / early 20th century.

Andrei Markov, 1856 - 1922, St Petersburg.

Amazingly, we will eventually be able to use Markov chains to help us with the grid search problem we encountered in Bayesian inference, but it will take some background to get there.

A Markov chain is a model of a system that evolves in time. For our purposes we will assume time is discrete, meaning that the system evolves in steps that can be denoted with integers.

At any given time, the Markov chain is in a particular state. The concept of a state is very flexible. We can use the idea of state to represent a lot of things: maybe a location in space, or a color, or a number of people in a room, or a particular value of a parameter. Anything that can be modeled as a discrete thing can be a state.

The basic idea of a Markov chain is that it moves from state to state probabilistically. In any state, there are certain probabilities of moving to each of the other states.

Definitions#

We will denote the state that the Markov chain is in at time $n$ as $X_n$. Since the Markov chain evolves probabilistically, $X_n$ is a random variable.

A defining aspect of a Markov chain is that each time it moves from the current state to the new state, the probability of that transition only depends on the current state.

This is called the Markov property.

The point is that whatever states the chain was in previously do not matter for determining where it goes next. Only the current state affects where the chain goes next.

Here is an abstract view of the situation at a particular node 0.

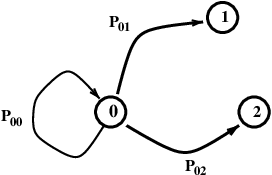
From state 0, on the next step the chain can go to state 1, state 2, or even back to state 0. There is a probability associated with each transition.

Note that the probabilities must sum to 1 – on each transition, the chain must go somewhere (even if it remains at the current node).

Definition. Given a finite set of states $S = \{1, 2, \dots \}$, a process $X_0, X_1, \dots$ is a Markov chain on $S$ if, when the process is in state $j$, the probability that its next state is $i$ depends only on $j$.

Formally, we say that

\[P(X_{n+1} = i \,\vert\, X_{n} = j, X_{n-1} = x_{n-1}, \dots, X_0 = x_0) = P(X_{n+1} = i \,\vert\, X_{n} = j).\]

This the formal statement of the Markov property.

It is usually convenient to work with Markov chains using linear algebra. For that, we use this notation:

Definition. The transition matrix of the chain is the matrix $P$ with $P_{ij} = P(X_{n+1} = i \,\vert\, X_{n} = j).$

Note that by the law of total probability, for any $j$:

\[ \sum_i P(X_{n+1} = i \,\vert\, X_{n} = j) = \sum_i P_{ij} = 1.\]

Hence, the columns of $P$ each sum to 1. Such a matrix is called a stochastic matrix.

Example 1. Let’s go back to our weather in Boston example

We can see that if at time $t=0$ the chain is in the “sunny” state, at time $t=1$ it will either be in a “sunny” state (with probability 0.8) or “rainy” state (with probability 0.6).

This chain has transition matrix:

\[\begin{split} P = \begin{bmatrix} .8 & .4 \\ .2 & .6 \\ \end{bmatrix} \end{split}\]

We can confirm that this is a stochastic matrix by observing that the columns sum to 1.

Example 2. Looking at a bigger, more abstract example, consider the Markov chain below, with states $\{0, 1, 2, 3\}$ and transition probabilities marked.

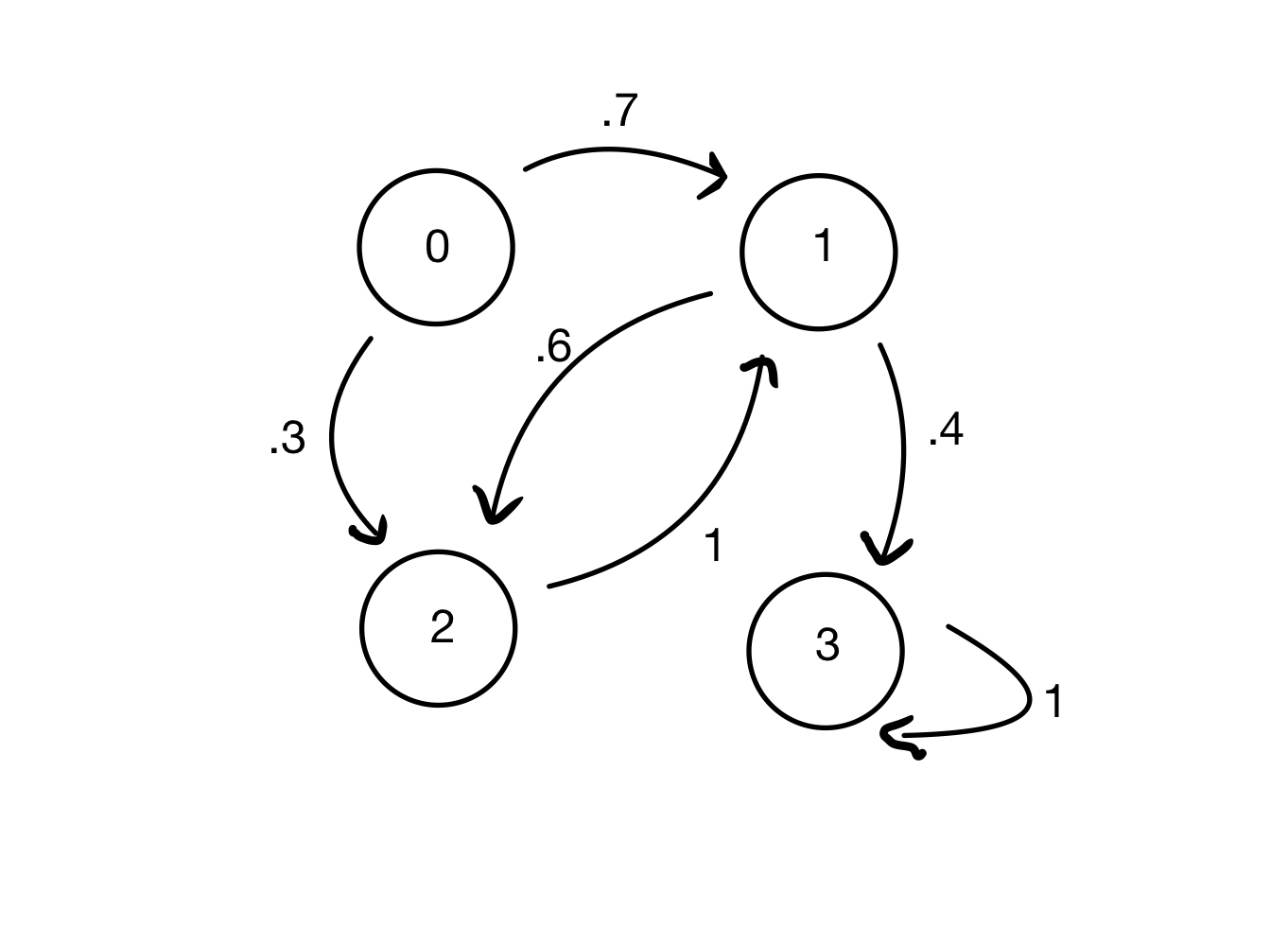
We can see that if at time $t= 0$ the chain is in state 1, at time $t = 1$ it will either be in state 2 (with probability 0.6) or state 3 (with probability 0.4).

This chain has transition matrix:

\[\begin{split} P = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0.7 & 0 & 1 & 0 \\ 0.3 & 0.6 & 0 & 0 \\ 0 & 0.4 & 0 & 1 \end{bmatrix} \end{split}\]

Again, we can confirm that this is a stochastic matrix by summing the columns.

Future States#

OK, so we know that if the chain is in state $j$, the probability that it will be in state $i$ at the next step is $P_{ij}$.

What is the probability it will be in state $i$ in two steps? three steps? $n$ steps?

Let’s define the $n$-step transition probability matrix $P^{(n)}$ as

\[ P^{(n)}_{ij} = P(X_n = i\,\vert\,X_0 = j). \]

How can we compute $P^{(n)}$?

Let’s compute it for the simple case of $n = 2$:

\[ P^{(2)}_{ij} = P(X_2 = i\,\vert\,X_0 = j) \]

\[ = \sum_k P(X_2 = i\,\vert\,X_1 = k, X_0 = j)\,P(X_1 = k\,\vert\,X_0 = j)\]

(This is by the law of total probability.)

which is then:

\[ = \sum_k P(X_2 = i\,\vert\,X_1 = k)\,P(X_1 = k\,\vert\,X_0 = j).\]

(By the Markov property)

Now let’s write the expression above in terms of matrices:

\[P^{(2)}_{ij} = \sum_k P_{ik}P_{kj}\]

Which turns out to be the definition of matrix multiplication.

So $$P(X_2 = i\,\vert\,X_0 = j) = P^{(2)}_{ij} = P^2_{ij} $$

In other words, the two-step transition probabilities are given by the square of the $P$ matrix.

You can see that this generalizes: the $n$-step transition probabilities are therefore given by the $n$th power of $P$.

\[P^{(n)} = P^n. \]

Example 1. Looking at weather in Boston again:

If at time $t=0$ the chain is in a “sunny” state, at time $t=2$ it will either be in “sunny” state (with probability 0.72) or a “rainy” state (with probability 0.28).

We can confirm that by computing $P^2$:

\[\begin{split} P^2 = \begin{bmatrix} 0.8 & 0.4 \\ 0.2 & 0.6 \\ \end{bmatrix} * \begin{bmatrix} 0.8 & 0.4 \\ 0.2 & 0.6 \\ \end{bmatrix} = \begin{bmatrix} 0.72 & .56 \\ 0.28 & 0.44 \\ \end{bmatrix} \end{split}\]

Example 2. And looking at our larger more abstract model again:

If at time $t= 0$ the chain is in state 1, at time $t = 2$ it will either be in state 1 (with probability 0.6) or state 3 (with probability 0.4).

We can confirm this by computing $P^2$:

\[\begin{split} P^2 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0.3 & 0.6 & 0 & 0 \\ 0.42 & 0 & 0.6 & 0 \\ 0.28 & 0.4 & 0.4 & 1 \end{bmatrix} \end{split}\]

Distributions Over States#

Now suppose we don’t know with certainty the initial state of the Markov chain, but rather we know a probabiity distribution over the initial states.

We will organize this distribution into a column vector $\mathbf{x}$. Since it is a distribution, the entries in $\mathbf{x}$ are nonnegative and sum to 1.

This distribution will evolve in time, so we will denote the distribution at time $n$ as $\mathbf{x}_n$.

In other words, $X_0$ is a random variable with distribution $P(X_0 = i) = \mathbf{x}_{0,i}$.

Now, we can show that taking one step forward in time corresponds to multiplying $P$ times $\mathbf{x}$ as follows:

\[ \mathbf{x}_{n+1,i} = P(X_{n+1} = i) = \sum_j P(X_{n+1} = i\,\vert\,X_n = j)\,P(X_n = j) \]

(by the law of total probability),

so

\[ \mathbf{x}_{n+1,i} = \sum_j P_{ij} \mathbf{x}_{n,j} \]

so

\[ \mathbf{x}_{n+1} = P\mathbf{x}_n. \]

This is called the Forward Kolmogorov Equation. This equation shows how to evolve the probability in time.

It is clear then that

\[ \mathbf{x}_n = P^n \mathbf{x}_0. \]

That is, if we know the initial probability distribution at time 0, we can find the distribution at any later time using powers of the matrix $P$.

Example 1.

If we say that an aribtrary day in Boston has an 80% chance of being sunny, we can calculate whether it will be sunny two days later.

We consider an initial probability distribution over states:

\[\begin{split} \mathbf{x}_0 = \begin{bmatrix}0.8\\0.2\end{bmatrix} \end{split}\]

Then to compute the distribution two days later, ie $\mathbf{x}_2,$ we can use $P^2$:

\[\begin{split} \mathbf{x}_2 = P^2\mathbf{x}_0 = \begin{bmatrix} 0.72 & .56 \\ 0.28 & 0.44 \\ \end{bmatrix} \, \begin{bmatrix}0.8\\0.2\end{bmatrix} = \begin{bmatrix}0.688\\0.312\end{bmatrix} \end{split}\]

Example 2.

Continuing our larger more abstract model again, if we consider an initial probability distribution over states:

\[\begin{split} \mathbf{x}_0 = \begin{bmatrix}0.1\\0.3\\0.2\\0.4\end{bmatrix} \end{split}\]

Then to compute the distribution two steps later, ie $\mathbf{x}_2,$ we can use $P^2$:

\[\begin{split} \mathbf{x}_2 = P^2\mathbf{x}_0 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0.3 & 0.6 & 0 & 0 \\ 0.42 & 0 & 0.6 & 0 \\ 0.28 & 0.4 & 0.4 & 1 \end{bmatrix} \, \begin{bmatrix}0.1\\0.3\\0.2\\0.4\end{bmatrix} = \begin{bmatrix}0\\0.21\\0.162\\0.628\end{bmatrix} \end{split}\]

Long Term Behavior#

One of the main questions we’ll be asking is concerned with the long run behavior of a Markov Chain.

Let’s consider the long run behavior of Boston weather. We start with just the knowledge that if today is sunny, tomorrow will be sunny with probability 0.8; otherwise it will be rainy. If today is rainy, tomorrow will be rainy with probabililty 0.6; otherwise it will be sunny.

We know we can calculate the probabilty of a sunny day in 2 days or in 10 days, but can we say anything interesting about the weather in 100 or 1,000 days?

Let’s start by writing out the one-step transition matrix for this problem:

\[\begin{split} P = \begin{bmatrix}0.8 & 0.4\\0.2 & 0.6\end{bmatrix}\end{split}\]

Now, let’s assume that day 0 is sunny, and let the chain “run” for a while:

# day 0 is sunny
x = np.array([1, 0])

# P is one-step transition matrix
P = np.array([[0.8, 0.4], [0.2, 0.6]])

for i in range(10):
    print (f'On day {i}, state is {x}')
    x = P @ x

On day 0, state is [1 0]
On day 1, state is [0.8 0.2]
On day 2, state is [0.72 0.28]
On day 3, state is [0.688 0.312]
On day 4, state is [0.6752 0.3248]
On day 5, state is [0.67008 0.32992]
On day 6, state is [0.668032 0.331968]
On day 7, state is [0.6672128 0.3327872]
On day 8, state is [0.66688512 0.33311488]
On day 9, state is [0.66675405 0.33324595]

This seems to be converging to a particular vector: $\begin{bmatrix} 2/3 \\ 1/3 \end{bmatrix}$.

What if instead, the chain starts from a rainy day?

# day 0 is rainy
x = np.array([0, 1])

# P is one-step transition matrix
P = np.array([[0.8, 0.4], [0.2, 0.6]])

for i in range(10):
    print (f'On day {i}, state is {x}')
    x = P @ x

On day 0, state is [0 1]
On day 1, state is [0.4 0.6]
On day 2, state is [0.56 0.44]
On day 3, state is [0.624 0.376]
On day 4, state is [0.6496 0.3504]
On day 5, state is [0.65984 0.34016]
On day 6, state is [0.663936 0.336064]
On day 7, state is [0.6655744 0.3344256]
On day 8, state is [0.66622976 0.33377024]
On day 9, state is [0.6664919 0.3335081]

Here too, the chain seems to be converging to the same vector $\begin{bmatrix} 2/3 \\ 1/3 \end{bmatrix}$.

This suggests that $\begin{bmatrix} 2/3 \\ 1/3 \end{bmatrix}$ is a special vector.

Indeed, we can see that if the chain ever exactly reached this vector, it would never deviate after that, because

\[\begin{split} \begin{bmatrix}0.8 & 0.4\\0.2 & 0.6\end{bmatrix} \begin{bmatrix} 2/3 \\ 1/3 \end{bmatrix} = \begin{bmatrix} 2/3 \\ 1/3 \end{bmatrix}\end{split}\]

A vector $\mathbf{x}$ for which $P \mathbf{x} = \mathbf{x}$ is called a steady state of the Markov chain $P$.

Example. If the Markov chain below is in state $\begin{bmatrix}\frac{6}{11}\\\frac{3}{11}\\\frac{2}{11}\end{bmatrix}$, is it in a steady state?

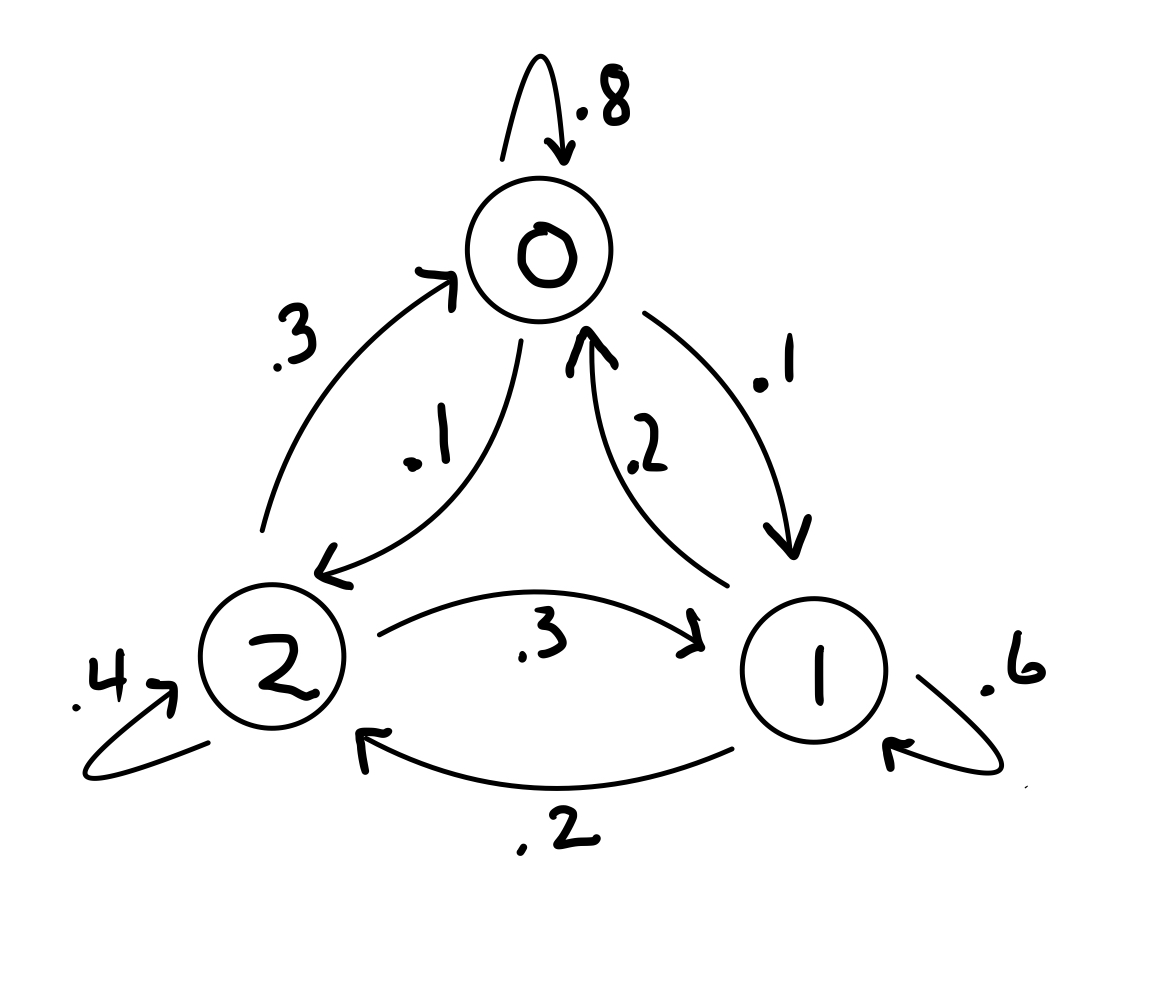
The transition matrix $P=\begin{bmatrix}0.8&0.2&0.3\\0.1&0.6&0.3\\0.1&0.2&0.4\end{bmatrix}$ and the state $x=\begin{bmatrix}\frac{6}{11}\\\frac{3}{11}\\\frac{2}{11}\end{bmatrix}$

We just need to check if $Px=x$

$$\begin{bmatrix}0.8&0.2&0.3\\0.1&0.6&0.3\\0.1&0.2&0.4\end{bmatrix} \begin{bmatrix}\frac{6}{11}\\\frac{3}{11}\\\frac{2}{11}\end{bmatrix}= \begin{bmatrix}\frac{6}{11}\\\frac{3}{11}\\\frac{2}{11}\end{bmatrix}$$.

So yes, the chain is in a steady state.

Convergence to Steady-State#

So, two remarkable things are happening in the example above:

There is a steady-state vector $\mathbf{x}$ such that $P\mathbf{x} = \mathbf{x}$.
It seems that the chain converges to this steady-state, no matter what the starting point is.

These properties are a very interesting and useful behavior, because it means we can talk about the long term behavior of the Markov Chain without worrying about what state the chain started in.

In particular this will turn out to be hugely useful for problems in Bayesian statistics (which we will return to in the next lecture).

So we would very much like to know

When does P have a steady-state?
When can we be sure that P converges to that steady state?

To answer these questions we’ll use a little bit of linear algebra and some ideas from the study of graphs.

~~~Extra Background Material for the Curious~~~

First, recall that when a square matrix $A$ has a nonzero vector $\mathbf{x}$ such that

\[ A\mathbf{x} = \lambda\mathbf{x} \]

for some scalar value $\lambda$, then we say that $\mathbf{x}$ is an eigenvector of $A$, and $\lambda$ is its associated eigenvalue.

Now $P$ has two special properties:

None of its entries are negative
Its columns sum to 1

Because of these two properties, we can prove that the largest eigenvalue $\lambda$ of $P$ is 1.

This is not hard to prove (and would be proved in a linear algebra course) but we’ll not prove it here. The key to proving it is based on the fact that the columns of $P$ sum to 1.

For $\lambda=1$ we see that $ A\mathbf{x} = \mathbf{x} $ making $x$ a steady state.

~~~End of Extra Background Material~~~

This means that every Markov chain has at least one steady-state.

OK, so next we’d like to establish whether the chain has a unique steady-state, that is, does it have only one steady-state?

Let’s consider the following Markov chain:

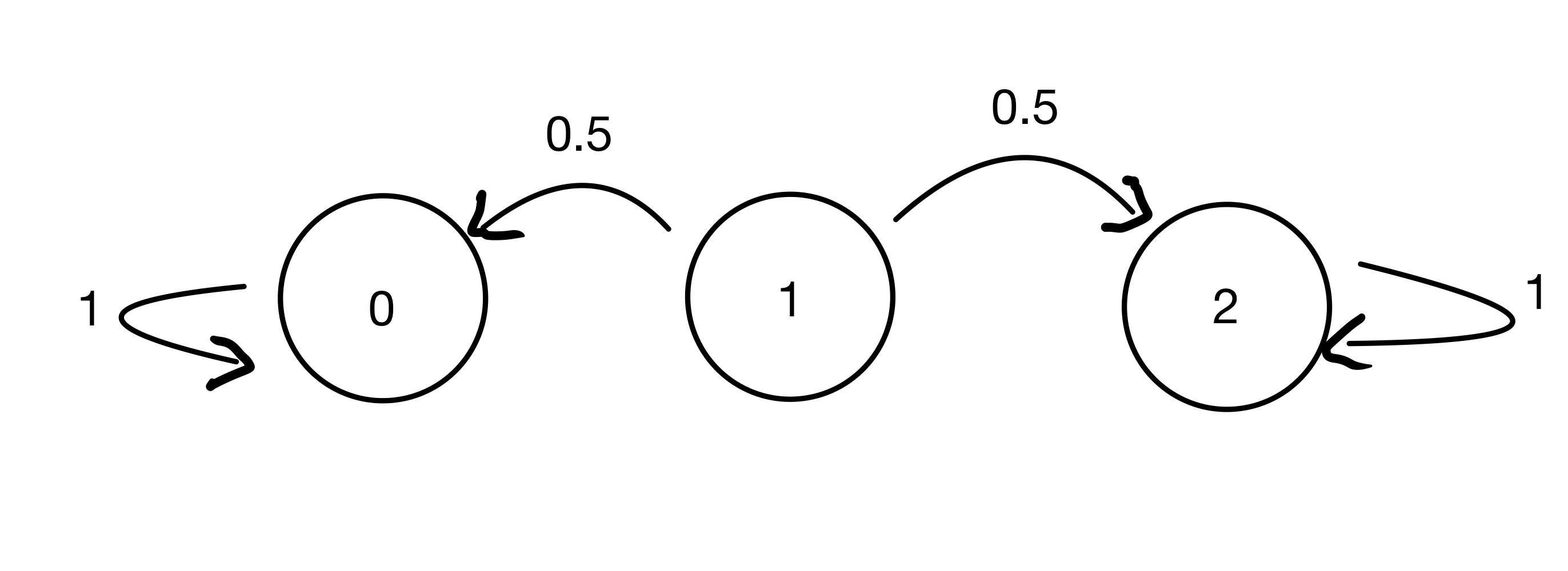
For this chain, the distribution $\begin{bmatrix}1\\0\\0\end{bmatrix}$ is a steady-state, as is the distribution $\begin{bmatrix}0\\0\\1\end{bmatrix}$.

In fact, any convex combination of these vectors is a steady state, such as $\begin{bmatrix}.6\\0\\.4\end{bmatrix}$.

So this Markov chain has an infinite set of steady-state vectors.

When does a Markov chain have just a single steady-state?

The key to the answer comes from looking at the graph above. Once the chain reaches state 0, it can never reach the other states in the future. Likewise for state 2.

We say that a state $i$ is reachable from state $j$ if one can get from $j$ to $i$ following directed edges.

Consider the previous example again:

Here, state 0 is not reachable from any other state.

Furthermore, state 3 can not reach any other state.

Now we can answer the question:

If in a Markov chain $P$, every state is reachable from every other state, we call the graph strongly connected. In that case, the Markov chain is irreducible, and it has only one steady-state.

Now, does an irreducible Markov chain always converge to its unique steady-state?

Consider this example:

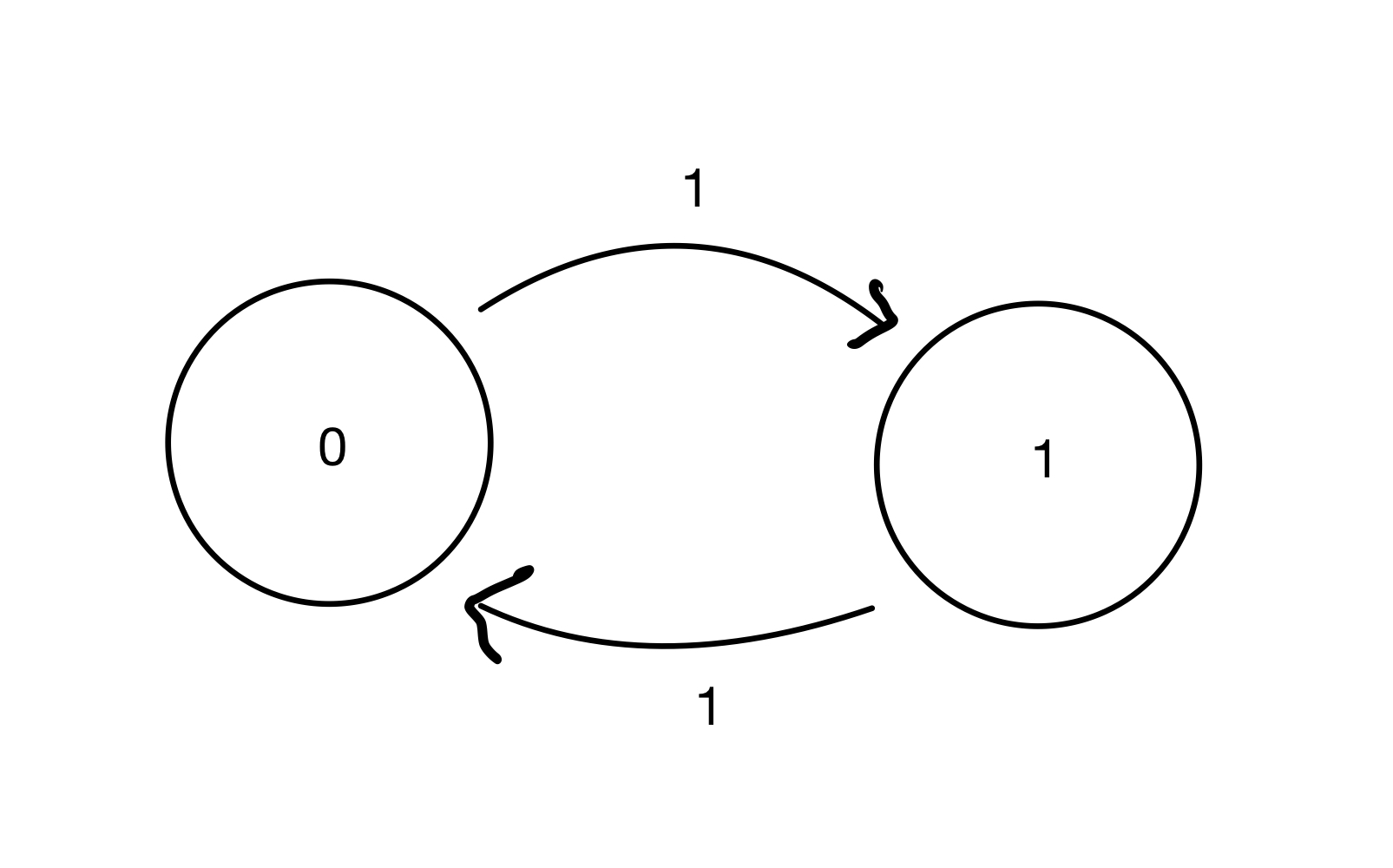
This chain is irreducible: each state can reach the other. So it has a unique steady-state, which is $\begin{bmatrix}0.5\\0.5\end{bmatrix}$.

However, it does not converge to that steady state.

Consider if it starts in state $\begin{bmatrix}1\\0\end{bmatrix}$. In the next step it will be $\begin{bmatrix}0\\1\end{bmatrix}$, and then back to $\begin{bmatrix}1\\0\end{bmatrix}$.

This cycle will continue forever.

Another way to think about this is that the future state of the Markov chain is never independent of its starting state.

So the Markov chain must not be periodic in the way that this example is.

There is a way to confirm that a Markov chain is not periodic.

A Markov chain is not periodic if there is some power of $P$, say $P^k$, such that all entries in $P^k$ are positive.

You can see that the transition matrix for the example above is

\[\begin{split} P = \begin{bmatrix}0&1\\1&0\end{bmatrix} \end{split}\]

and you can confirm that no power of $P$ is all positive.

When a Markov chain $P$ has some power $k$ such that all entries in $P^k$ are positive, then the chain is said to be primitive.

And now we can complete the story:

A primitive (i.e. irreducible aperiodic) Markov chain has a single steady-state to which it always converges.

Example. In the following chain, for each node, all transitions out of that node are equally probable. So for a node with 2 outgoing transitions, the probabilities are each 1/2. Is this chain a primitive Markov Chain?

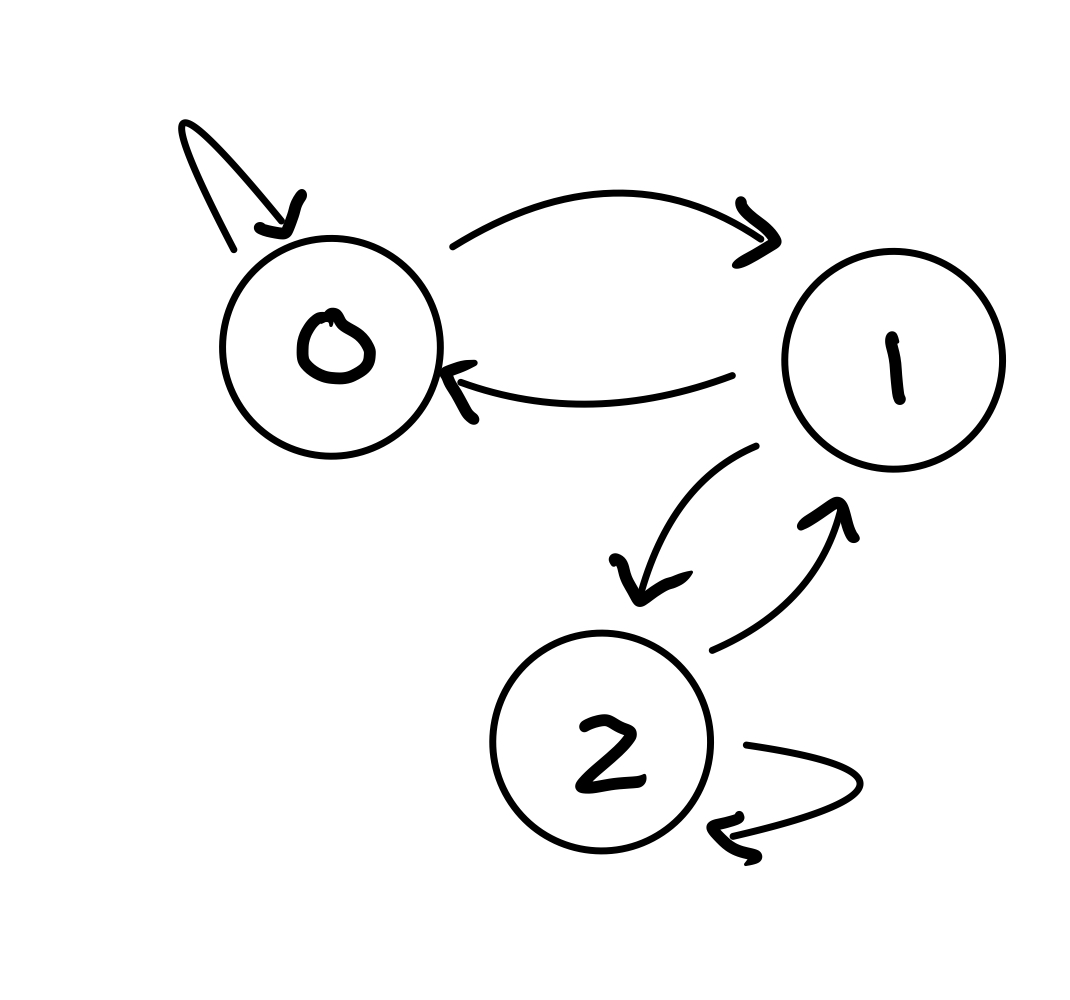
First, is it a Markov chain?

We need to check if the columns add up to 1.

\[\begin{split}P = \begin{bmatrix}0.5&0.5&0\\0.5&0&0.5\\0&0.5&0.5\end{bmatrix}\end{split}\]

Second, does it have at least one steady state?

Yes, all Markov chains have at least one steady state.

Third, does it have exactly one steady state?

We need to check if every state is reachable from every other state

Does it converege to that steady state?

We need to check if our Markov chain $P$ has some power $k$ such that all entries in $P^k$ are positive

Let’s check $k=2$ first:

\[\begin{split}P^2 = \begin{bmatrix}0.5&0.5&0\\0.5&0&0.5\\0&0.5&0.5\end{bmatrix} \begin{bmatrix}0.5&0.5&0\\0.5&0&0.5\\0&0.5&0.5\end{bmatrix} = \begin{bmatrix}0.5&0.25&0.25\\0.25&0.5&0.25\\0.25&0.5&0.25\end{bmatrix}\end{split}\]

We already see only positive entries in $P^2$ so the Markov chain convereges.

Therefore our example is indeed a primitive Markov chain.

Time Averages and Ensemble Averages#

There are two senses in which we can interpret the steady-state of a Markov chain.

~~~Extra Background Material for the Curious~~~

Say we have a Markov chain with steady-state vector $\mathbf{x}$.

First, consider the evolution of states $X_0, X_1, \dots.$ At some time long in the future, the probability that the chain is in state $i$ is given by component $i$ of $\mathbf{x}$. We say that the steady-state represents the time average state, because if we observe the Markov chain over a sequence of steps while it is in steady-state, component $i$ of $\mathbf{x}$ tells us how often we will see it in state $i$.

In contrast, consider if we observed many copies of $P$ evolving in parallel. At some time long in the future, we stop all the chains and look at the distribution of states they are in. This is called the ensemble average of the Markov chain.

~~~End of Extra Background Material~~~

It is a wonderful fact that for a primitive Markov chain (with a finite state space), the time average and the ensemble average are the same. This is going to be very helpful for us.

The property of having identical time average and ensemble average is called ergodicity.

So we can say that a primitive Markov chain is ergodic