import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import sklearn.datasets as sk_data
from sklearn.cluster import KMeans

#import matplotlib as mpl
import seaborn as sns
%matplotlib inline

Hierarchical Clustering#

Today we will look at a fairly different approach to clustering.

So far, we have been thinking of clustering as finding a partition of our dataset.

That is, a set of nonoverlapping clusters, in which each data item is in one cluster.

However, in many cases, the notion of a strict partition is not as useful.

How Many Clusters?#

How many clusters would you say there are here?

X_rand, y_rand = sk_data.make_blobs(n_samples=[100, 100, 250, 70, 75, 80], centers = [[1, 2], [1.5, 1], [3, 2], [1.75, 3.25], [2, 4], [2.25, 3.25]], n_features = 2,
                          center_box = (-10.0, 10.0), cluster_std = [.2, .2, .3, .1, .15, .15], random_state = 0)
df_rand = pd.DataFrame(np.column_stack([X_rand[:, 0], X_rand[:, 1], y_rand]), columns = ['X', 'Y', 'label'])
df_rand = df_rand.astype({'label': 'int'})
df_rand['label2'] = [{0: 0, 1: 1, 2: 2, 3: 3, 4: 3, 5: 3}[x] for x in df_rand['label']]
df_rand['label3'] = [{0: 0, 1: 0, 2: 1, 3: 2, 4: 2, 5: 2}[x] for x in df_rand['label']]
# kmeans = KMeans(init = 'k-means++', n_clusters = 3, n_init = 100)
# df_rand['label'] = kmeans.fit_predict(df_rand[['X', 'Y']])

df_rand.plot('X', 'Y', kind = 'scatter',  
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off');

_images/08-Clustering-III-hierarchical_6_0.png

Three clusters?

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label3', colormap='viridis', 
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off');

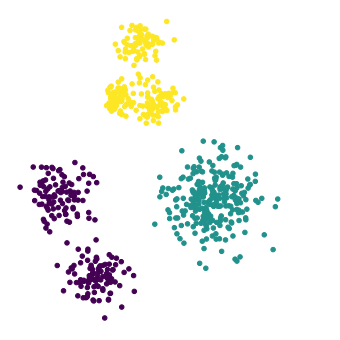
_images/08-Clustering-III-hierarchical_8_0.png

Four clusters?

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label2', colormap='viridis', 
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off');

_images/08-Clustering-III-hierarchical_10_0.png

Six clusters?

df_rand.plot('X', 'Y', kind = 'scatter', c = 'label', colormap='viridis', 
                   colorbar = False, figsize = (6, 6))
plt.axis('square')
plt.axis('off');

_images/08-Clustering-III-hierarchical_12_0.png

This dataset shows clustering on multiple scales.

To fully capture the structure in this dataset, two things are needed:

Capturing the differing clusters depending on the scale
Capturing the containment relations – which clusters lie within other clusters

These observations motivate the notion of hierarchical clustering.

In hierarchical clustering, we move away from the partition notion of \(k\)-means,

and instead capture a more complex arrangement that includes containment of one cluster within another.

Hierarchical Clustering#

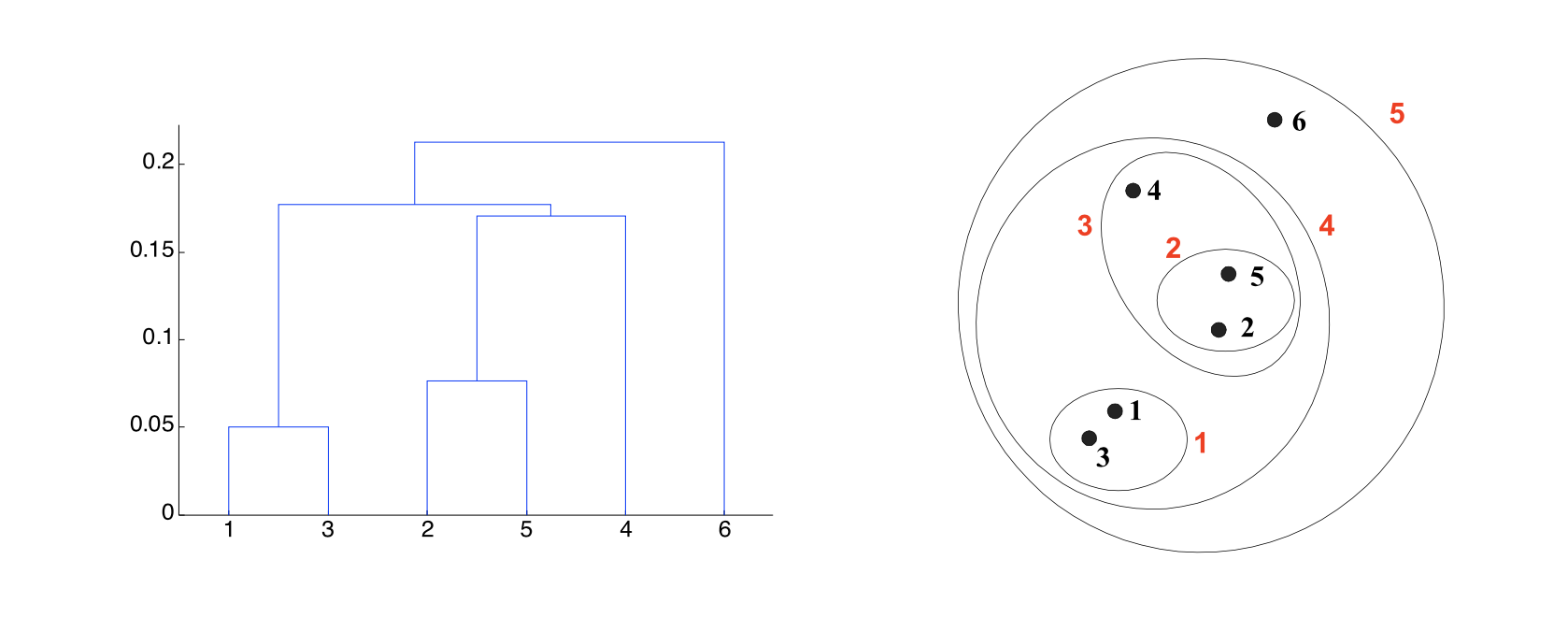
A hierarchical clustering produces a set of nested clusters organized into a tree.

A hierarchical clustering is visualized using a dendrogram

A tree-like diagram that records the containment relations among clusters.

Strengths of Hierarchical Clustering#

Hierarchical clustering has a number of advantages:

First, a hierarchical clustering encodes many different clusterings. That is, it does not itself decide on the correct number of clusters.

A clustering is obtained by “cutting” the dendrogram at some level.

This means that you can make this crucial decision yourself, by inspecting the dendrogram.

Put another way, you can obtain any desired number of clusters.

The second advantage is that the dendrogram may itself correspond to a meaningful structure, for example, a taxonomy.

The third advantage is that many hierarchical clustering methods can be performed using either similarity (proximity) or dissimilarity (distance) metrics.

This can be very helpful!

(Note that techniques like \(k\)-means cannot be used with unmodified similarity metrics.)

Compared to \(k\)-means#

Another aspect of hierachical clustering is that it can handle certain cases better than \(k\)-means.

Because of the nature of the \(k\)-means algorithm, \(k\)-means tends to produce:

Roughly spherical clusters
Clusters of approximately equal size
Non-overlapping clusters

In many real-world situations, clusters may not be round, they may be of unequal size, and they may overlap.

Hence we would like clustering algorithms that can work in those cases also.

Hierarchical Clustering Algorithms#

There are two main approaches to hierarchical clustering: “bottom-up” and “top-down.”

Agglomerative Clustering (“bottom-up”):

Start by defining each point as its own cluster
At each successive step, merge the two clusters that are closest to each other
Repeat until only one cluster is left.

Divisive Clustering (“top-down”):

Start with one, all-inclusive cluster
At each step, find the cluster split that creates the largest distance between resulting clusters
Repeat until each point is in its own cluster.

Agglomerative techniques are by far the more common.

The key to both of these methods is defining the distance between two clusters.

Different definitions for the inter-cluster distance yield different clusterings.

To illustrate the impact of the choice of cluster distances, we’ll focus on agglomerative clustering.

Defining Cluster Proximity#

Given two clusters, how do we define the distance between them?

Here are three natural ways to do it:

Single-Linkage: the distance between two clusters is the distance between the closest two points that are in different clusters.

\[ D_\text{single}(i,j) = \min_{x, y}\{d(x, y) \,|\, x \in C_i, y \in C_j\}\]

Complete-Linkage: the distance between two clusters is the distance between the farthest two points that are in different clusters.

\[ D_\text{complete}(i,j) = \max_{x, y}\{d(x, y) \,|\, x \in C_i, y \in C_j\}\]

Average-Linkage: the distance between two clusters is the average distance between all pairs of points from different clusters.

\[ D_\text{average}(i,j) = \frac{1}{|C_i|\cdot|C_j|}\sum_{x \in C_i,\, y \in C_j}d(x, y)\]

Single-Linkage

Complete-Linkage

Average-Linkage

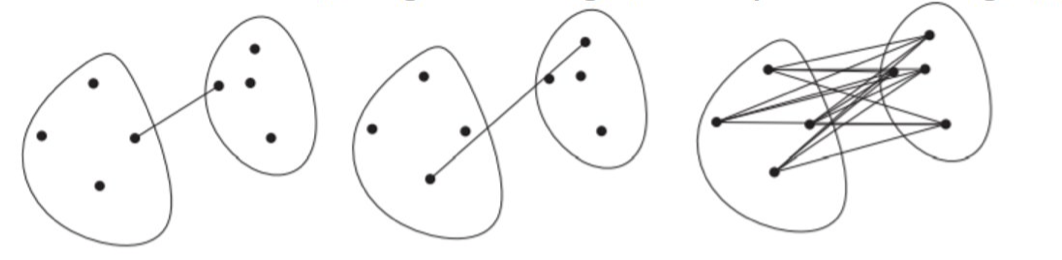
Notice that it is easy to express the definitions above in terms of similarity instead of distance.

Here is a set of 6 points that we will cluster to show differences between distance metrics.

pt_x = [0.4, 0.22, 0.35, 0.26, 0.08, 0.45]
pt_y = [0.53, 0.38, 0.32, 0.19, 0.41, 0.30]
plt.plot(pt_x, pt_y, 'o', markersize = 10, color = 'k')
plt.ylim([.15, .60])
plt.xlim([0.05, 0.70])
for i in range(6):
    plt.annotate(f'{i}', (pt_x[i]+0.02, pt_y[i]-0.01), fontsize = 12)
plt.axis('off')
plt.savefig('figs/L08-basic-pointset.png');

_images/08-Clustering-III-hierarchical_44_0.png

X = np.array([pt_x, pt_y]).T
from scipy.spatial import distance_matrix
labels = ['p0', 'p1', 'p2', 'p3', 'p4', 'p5']
D = pd.DataFrame(distance_matrix(X, X), index = labels, columns = labels)
D.style.format('{:.2f}')

	p0	p1	p2	p3	p4	p5
p0	0.00	0.23	0.22	0.37	0.34	0.24
p1	0.23	0.00	0.14	0.19	0.14	0.24
p2	0.22	0.14	0.00	0.16	0.28	0.10
p3	0.37	0.19	0.16	0.00	0.28	0.22
p4	0.34	0.14	0.28	0.28	0.00	0.39
p5	0.24	0.24	0.10	0.22	0.39	0.00

Single-Linkage Clustering#

import scipy.cluster
import scipy.cluster.hierarchy as hierarchy
Z = hierarchy.linkage(X, method='single')
hierarchy.dendrogram(Z);

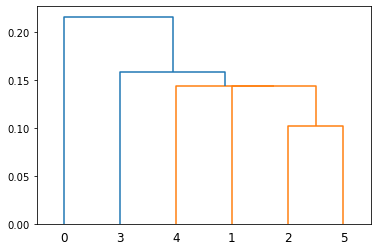
_images/08-Clustering-III-hierarchical_48_0.png

Advantages:

Single-linkage clustering can handle non-elliptical shapes.

In fact it can produce long, elongated clusters:

X_moon_05, y_moon_05 = sk_data.make_moons(random_state = 0, noise = 0.05)
Z = hierarchy.linkage(X_moon_05, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_moon_05[:,0], X_moon_05[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Single-Linkage Can Find Irregularly Shaped Clusters')
plt.axis('off');

_images/08-Clustering-III-hierarchical_50_0.png

X_rand_lo, y_rand_lo = sk_data.make_blobs(n_samples=[20, 200], centers = [[1, 1], [3, 1]], n_features = 2,
                          center_box = (-10.0, 10.0), cluster_std = [.1, .5], random_state = 0)
Z = hierarchy.linkage(X_rand_lo, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_rand_lo[:,0], X_rand_lo[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Single-Linkage Can Find Different-Sized Clusters')
plt.axis('off');

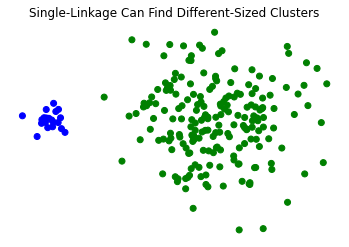
_images/08-Clustering-III-hierarchical_51_0.png

Disadvantages:

Single-linkage clustering can be sensitive to noise and outliers.

X_moon_10, y_moon_10 = sk_data.make_moons(random_state = 0, noise = 0.1)
Z = hierarchy.linkage(X_moon_10, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_moon_10[:,0], X_moon_10[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Single-Linkage Clustering Changes Drastically on Slightly More Noisy Data')
plt.axis('off');

_images/08-Clustering-III-hierarchical_53_0.png

X_rand_hi, y_rand_hi = sk_data.make_blobs(n_samples=[20, 200], centers = [[1, 1], [3, 1]], n_features = 2,
                          center_box = (-10.0, 10.0), cluster_std = [.15, .6], random_state = 0)
Z = hierarchy.linkage(X_rand_hi, method='single')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.title('Single-Linkage Clustering Changes Drastically on Slightly More Noisy Data')
plt.scatter(X_rand_hi[:,0], X_rand_hi[:,1], c = [['b','g'][i-1] for i in labels])
plt.axis('off');

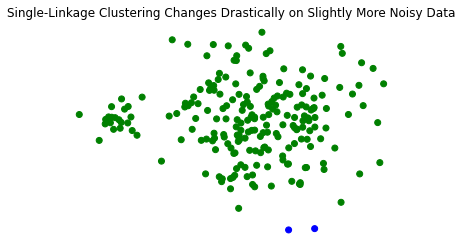
_images/08-Clustering-III-hierarchical_54_0.png

Complete-Linkage Clustering#

Z = hierarchy.linkage(X, method='complete')
hierarchy.dendrogram(Z);

_images/08-Clustering-III-hierarchical_57_0.png

Advantages:

Produces more-balanced clusters – more-equal diameters

X_moon_05, y_moon_05 = sk_data.make_moons(random_state = 0, noise = 0.05)
Z = hierarchy.linkage(X_moon_05, method='complete')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_moon_05[:,0], X_moon_05[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Complete-Linkage Seeks Globular Clusters of Similar Size')
plt.axis('off');

_images/08-Clustering-III-hierarchical_59_0.png

Z = hierarchy.linkage(X_rand_hi, method='complete')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_rand_hi[:,0], X_rand_hi[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Complete-Linkage Seeks Globular Clusters of Similar Size')
plt.axis('off');

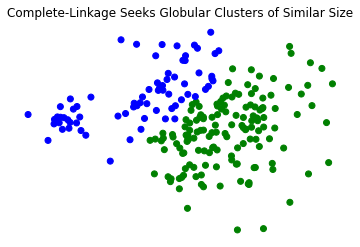
_images/08-Clustering-III-hierarchical_60_0.png

Less susceptible to noise:

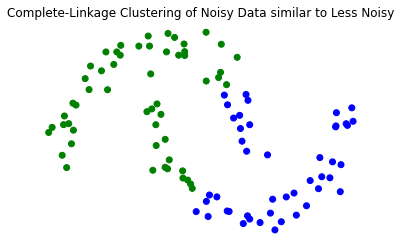
Z = hierarchy.linkage(X_moon_10, method='complete')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_moon_10[:,0], X_moon_10[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Complete-Linkage Clustering of Noisy Data similar to Less Noisy')
plt.axis('off');

_images/08-Clustering-III-hierarchical_62_0.png

Average-Linkage Clustering#

Z = hierarchy.linkage(X, method='average')
hierarchy.dendrogram(Z);

_images/08-Clustering-III-hierarchical_65_0.png

Average-Linkage clustering is in some sense a compromise between Single-linkage and Complete-linkage clustering.

Strengths:

Less susceptible to noise and outliers

Limitations:

Biased toward elliptical clusters

Z = hierarchy.linkage(X_moon_10, method='average')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_moon_10[:,0], X_moon_10[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Average-Linkage Similar to Complete - Globular Clusters')
plt.axis('off');

_images/08-Clustering-III-hierarchical_67_0.png

Z = hierarchy.linkage(X_rand_hi, method='average')
labels = hierarchy.fcluster(Z, 2, criterion = 'maxclust')
plt.scatter(X_rand_hi[:,0], X_rand_hi[:,1], c = [['b','g'][i-1] for i in labels])
plt.title('Average-Linkage More resistant to noise than Single-Linkage')
plt.axis('off');

_images/08-Clustering-III-hierarchical_68_0.png

All Three Compared#

Single-Linkage

Complete-Linkage

Average-Linkage

Ward’s Distance#

Finally, we consider one more cluster distance.

Ward’s distance asks “what if”.

That is, “What if we combined these two clusters – how would clustering improve?”

To define “how would clustering improve?” we appeal to the \(k\)-means criterion.

So:

Ward’s Distance between clusters \(C_i\) and \(C_j\) is the difference between the total within cluster sum of squares for the two clusters separately, compared to the within cluster sum of squares resulting from merging the two clusters into a new cluster \(C_{i+j}\):

\[D_\text{Ward}(i, j) = \sum_{x \in C_i} (x - r_i)^2 + \sum_{x \in C_j} (x - r_j)^2 - \sum_{x \in C_{i+j}} (x - r_{i+j})^2 \]

where \(r_i, r_j, r_{i+j}\) are the corresponding cluster centroids.

In a sense, this cluster distance results in a hierarchical analog of \(k\)-means.

As a result, it has properties similar to \(k\)-means:

Less susceptible to noise and outliers
Biased toward elliptical clusters

Hence it tends to behave more like group-average hierarchical clustering.

Hierarchical Clustering In Practice#

Now we’ll look at doing hierarchical clustering in practice, using python.

We’ll use the same synthetic data as we did in the k-means case – ie., three “blobs” living in 30 dimensions.

X, y = sk_data.make_blobs(n_samples=100, centers=3, n_features=30,
                          center_box=(-10.0, 10.0),random_state=0)

As a reminder of the raw data here is the visualization: first the raw data, then an embedding into 2-D (using MDS).

sns.heatmap(X, xticklabels=False, yticklabels=False, linewidths=0,cbar=False);

_images/08-Clustering-III-hierarchical_82_0.png

import sklearn.manifold
import sklearn.metrics as metrics
euclidean_dists = metrics.euclidean_distances(X)
mds = sklearn.manifold.MDS(n_components = 2, max_iter = 3000, eps = 1e-9, random_state = 0,
                   dissimilarity = "precomputed", n_jobs = 1)
fit = mds.fit(euclidean_dists)
pos = fit.embedding_
plt.axis('equal')
plt.scatter(pos[:, 0], pos[:, 1], s = 8);

_images/08-Clustering-III-hierarchical_83_0.png

Hierarchical clustering is available in sklearn, but there is a much more fully developed set of tools in the scipy package and that is the one to use.

import scipy.cluster
import scipy.cluster.hierarchy as hierarchy
import scipy.spatial.distance

# linkages = ['single','complete','average','weighted','ward']
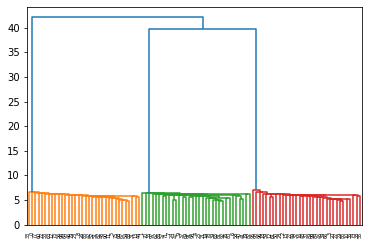
Z = hierarchy.linkage(X, method = 'single')

R = hierarchy.dendrogram(Z)

_images/08-Clustering-III-hierarchical_86_0.png

Hierarchical Clustering Real Data#

Once again we’ll use the “20 Newsgroup” data provided as example data in sklearn.

(http://scikit-learn.org/stable/datasets/twenty_newsgroups.html).

from sklearn.datasets import fetch_20newsgroups
categories = ['comp.os.ms-windows.misc', 'sci.space','rec.sport.baseball']
news_data = fetch_20newsgroups(subset = 'train', categories = categories)

from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(stop_words='english', min_df = 4, max_df = 0.8)
data = vectorizer.fit_transform(news_data.data).todense()
data.shape

(1781, 9409)

# metrics can be ‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, 
# ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘matching’, 
# ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, 
# ‘sqeuclidean’, ‘yule’.
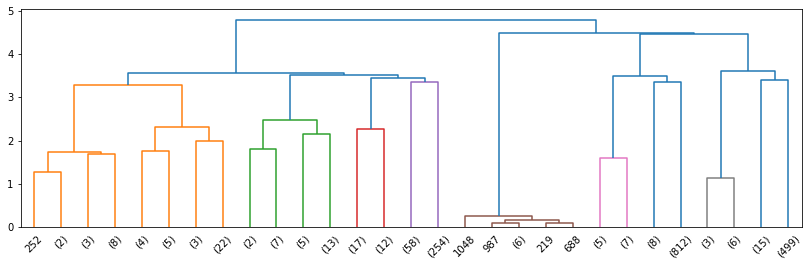
Z_20ng = hierarchy.linkage(data, method = 'ward', metric = 'euclidean')
plt.figure(figsize=(14,4))
R_20ng = hierarchy.dendrogram(Z_20ng, p=4, truncate_mode = 'level', show_leaf_counts=True)

_images/08-Clustering-III-hierarchical_91_0.png

Selecting the Number of Clusters#

clusters = hierarchy.fcluster(Z_20ng, 3, criterion = 'maxclust')
print(clusters.shape)
clusters

(1781,)

array([3, 3, 3, ..., 1, 3, 1], dtype=int32)

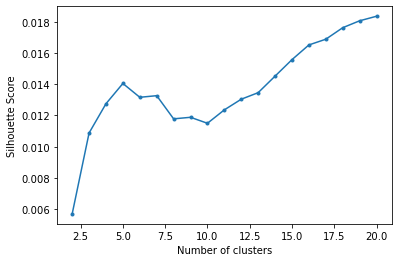
max_clusters = 20
s = np.zeros(max_clusters+1)
for k in range(2, max_clusters+1):
    clusters = hierarchy.fcluster(Z_20ng, k, criterion = 'maxclust')
    s[k] = metrics.silhouette_score(np.asarray(data), clusters, metric = 'euclidean')
plt.plot(range(2, len(s)), s[2:], '.-')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score');

_images/08-Clustering-III-hierarchical_94_0.png

print('Top Terms Per Cluster:')
k = 5
clusters = hierarchy.fcluster(Z_20ng, k, criterion = 'maxclust')
for i in range(1,k+1):
    items = np.array([item for item,clust in zip(data, clusters) if clust == i])
    centroids = np.squeeze(items).mean(axis = 0)
    asc_order_centroids = centroids.argsort()#[:, ::-1]
    order_centroids = asc_order_centroids[::-1]
    terms = vectorizer.get_feature_names_out()
    print(f'Cluster {i}:')
    for ind in order_centroids[:10]:
        print(f' {terms[ind]}')
    print('')

Top Terms Per Cluster:
Cluster 1:
 space
 nasa
 edu
 henry
 gov
 alaska
 access
 com
 moon
 digex

Cluster 2:
 ax
 max
 b8f
 g9v
 a86
 145
 1d9
 pl
 2di
 0t

Cluster 3:
 edu
 com
 year
 baseball
 article
 writes
 cs
 team
 game
 university

Cluster 4:
 risc
 instruction
 ghhwang
 csie
 set
 nctu
 cisc
 tw
 reduced
 mq

Cluster 5:
 windows
 edu
 file
 dos
 com
 files
 card
 drivers
 driver
 use

Tools for Data Science

Hierarchical Clustering

Contents

Hierarchical Clustering#

How Many Clusters?#

Hierarchical Clustering#

Strengths of Hierarchical Clustering#

Compared to \(k\)-means#

Hierarchical Clustering Algorithms#

Defining Cluster Proximity#

Single-Linkage Clustering#

Complete-Linkage Clustering#

Average-Linkage Clustering#

All Three Compared#

Ward’s Distance#

Hierarchical Clustering In Practice#

Hierarchical Clustering Real Data#

Selecting the Number of Clusters#